1102. Задача с
палочками
Хуанхан имеет
n палочек разной длины. Однажды она выложила их в ряд, длины
которых равны s1, s2, s3, ..., sn. После
измерения каждой палочки sk (1 ≤ k ≤ n) она заметила, что для некоторых
пар палочек si и sj (1 ≤ i < j ≤ n) длина каждой палочки, расположенной между si и sj, строго больше
si и строго меньше sj.
По заданной
последовательности длин s1, s2, s3, ...sn найдите наибольшее возможное значение разности j – i.
Вход. Состоит из
нескольких тестов. Каждый тест состоит из двух строк. Первая строка содержит
количество палочек n (n ≤ 50000). Вторая строка содержит n
различных натуральных чисел (не превосходящих 105) – длины палочек.
Выход. Для каждого
теста выведите в отдельной строке наибольшее значение j – i. Если таких индексов i и j не существует, выведите -1.
|
Пример входа |
Пример выхода |
|
4 5 4 3 6 4 6 5 4 3 9 12 4 8 7 5 9
6 3 1 |
1 -1 4 |
РЕШЕНИЕ
RMQ
+ бинарный поиск
Анализ алгоритма
Для каждого индекса i находим
максимальный индекс k (i ≤ k ≤ n), для которого RMinQ(si+1,
…, sk) > si. Это можно сделать с помощью бинарного поиска. Далее искомый индекс j определяется как позиция,
на которой достигается значение RMaxQ(si,
…, sk) при i ≤ j ≤ k.
Таким образом, для каждого индекса i следует
найти максимально возможный индекс j, после чего среди всех найденных
пар (i, j) определить наибольшую разность j – i.
Пример
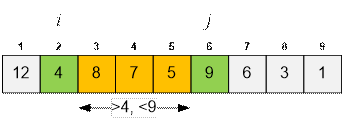
Рассмотрим третий пример.
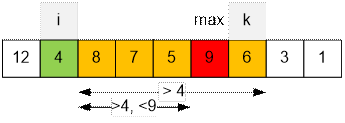
Пусть i = 2 (s2
= 4).
Наибольшим является индекс k = 7, для которого выполняется условие RMinQ(si+1, …, sk) > 4. Значение RMaxQ(s3, …, s7)
достигается на индексе j = 6.
Реализация
алгоритма
Объявим
константы и массивы.
#define MAX 50010
#define LOGMAX 16
int dp_max[MAX][LOGMAX], dp_min[MAX][LOGMAX];
int a[MAX];
Функция Build_RMQ_Array строит RMQ таблицы для быстрых запросов минимума (dp_min) и максимума (dp_max):
·
dp_min[i][j] содержит минимальное
значение на отрезке длиной 2j, начиная с позиции i.
·
dp_max[i][j] содержит индекс элемента с
максимальным значением на отрезке длиной 2j, начиная с i.
void Build_RMQ_Array(int
*b)
{
int i, j;
for (i = 1; i
<= n; i++)
{
dp_min[i][0] = b[i];
dp_max[i][0] = i;
}
for (j = 1; 1
<< j <= n; j++)
for (i = 1;
i + (1 << j) - 1 <= n; i++)
{
if
(b[dp_max[i][j - 1]] > b[dp_max[i + (1 << (j - 1))][j - 1]])
dp_max[i][j] = dp_max[i][j - 1];
else
dp_max[i][j] = dp_max[i + (1 <<
(j - 1))][j - 1];
dp_min[i][j] =
min(dp_min[i][j - 1], dp_min[i + (1
<< (j - 1))][j - 1]);
}
}
Функция RangeMaxQuery находит индекс максимального элемента на подотрезке [i,
j].
int RangeMaxQuery(int
i, int j)
{
int k = 0;
while ((1
<< (k + 1)) <= j - i + 1) k++;
if
(a[dp_max[i][k]] > a[dp_max[j - (1<<k) + 1][k]])
return
dp_max[i][k];
else
return
dp_max[j - (1<<k) + 1][k];
}
Функция RangeMinQuery находит минимальное
значение на подотрезке [i, j].
int RangeMinQuery(int
i, int j)
{
int k = 0;
while ((1
<< (k + 1)) <= j - i + 1) k++;
return
min(dp_min[i][k],dp_min[j - (1<<k) + 1][k]);
}
Функция BinSearch с помощью бинарного поиска на интервале [Left; Right] находит наибольший индекс k, для
которого все элементы между Left + 1 и k больше, чем a[Left].
int BinSearch(int
Left, int Right)
{
int MinValue
= a[Left++];
if
(RangeMinQuery(Left,Right) > MinValue) return
Right;
while (Right
> Left)
{
int Middle
= (Left + Right) / 2;
if
(RangeMinQuery(Left,Middle) > MinValue)
Left = Middle + 1;
else
Right = Middle;
}
if
(dp_min[Left][0] <= MinValue) Left--;
return Left;
}
Основная
часть программы. Последовательно обрабатываем тесты.
while(scanf("%d",&n)
== 1)
{
for(i = 1; i <= n; i++) scanf("%d",&a[i]);
Строим RMinQ и RMaxQ массивы.
Build_RMQ_Array(a);
Для каждого индекса i:
·
с
помощью BinSearch(i, n) находим наибольший индекс k, где все элементы на
интервале [i
+ 1; k] больше a[i];
·
на
интервале [i, k] находим индекс j, на котором достигается максимум.
·
проверяем,
не является ли j – i наибольшей разницей.
res = 0;
for(i = 1; i
<= n; i++)
{
k = BinSearch(i, n);
j = RangeMaxQuery(i,k);
if (j - i
> res) res = j - i;
}
Выводим ответ. В случае res = 0 выводить следует -1.
if (res == 0)
res = -1;
printf("%d\n",res);
}